1916년 11월 5일, 알베르트 아인슈타인이 독일의 과학학술지인 ‘물리학 연보’에 “우주는 비유클리드 기하학인 리만기하학에 의해서만 분석가능한 휜 공간”이라는 일반상대성이론 발표
알베르트 아인슈타인 (Albert Einstein, 독: Albert Einstein, 1879년 3월 14일 ~ 1955년 4월 18일)은 1905년 6월 30일 ‘특수 상대성이론’ (特殊相對性理論, theory of special relativity; 또는 ‘특수상대론’ 特殊相對論, special relativity)에 대한 논문을 발표했다.

이어 1916년 11월 5일, 알베르트 아인슈타인은 독일의 과학학술지인 ‘물리학 연보’에 일반상대성이론을 발표하며 “우주는 비유클리드 기하학인 리만기하학에 의해서만 분석가능한 휜 공간”이라고 주장했다.
일반 상대성이론 (一般相對性理論, theory of general relativity, 독: allgemeine Relativitätstheorie) 또는 일반상대론 (一般相對論, general relativity)은 마르셀 그로스만, 다비드 힐베르트, 알베르트 아인슈타인 등에 의해 발전되고 아인슈타인과 힐베르트가 1915년에 발표한, 중력을 상대론적으로 다루는 물리학 이론이다.
핀란드의 이론물리학자 노르드스트룀도 일반 상대론의 많은 부분을 논문으로 발표했었다.
일반 상대론은 현재까지 알려진, 중력을 다루는 이론 가운데 가장 정확하게 실험적으로 검증되었다.
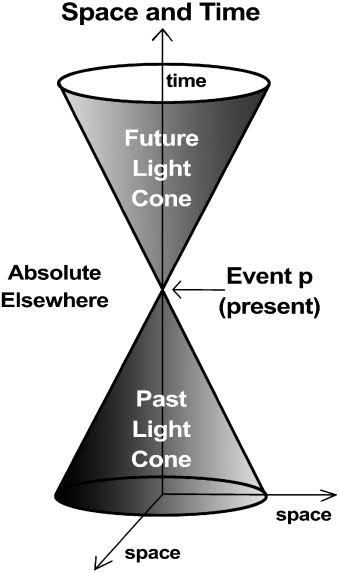
특수 상대성 이론에서 수학자 헤르만 민코프스키가 민코프스키 공간을 도입하여 평평한 시공간을 기하학적으로 다루었다.
일반 상대성 이론은 중력의 영향을 시공간의 휘어짐으로 기술한다.
일반상대론에서 시공간의 수학적 구조는 특별한 종류의 준 리만 다양체이며 국소적 (locally)으로 민코프스키 공간이다.
시공간의 휘어짐은 수학적으로 준 리만 다양체의 곡률에 해당한다 (더 정확히는 준 리만 다양체 중에서도 특수한 로런츠 다양체의 곡률).

즉, 일반상대론은 1850년대에 만들어진 수학인 리만 기하학으로 기술된다.
시공의 곡률 (아인슈타인 텐서)은 (우주 상수를 무시하면) 4차원 운동량 밀도에 비례하는데, 이를 아인슈타인 방정식이라고 한다.
일반 상대성 이론에서는 관성계뿐만 아니라 비관성계를 포함한 임의의 좌표계에 대해 물리 법칙이 동등한 형태를 유지하여야 한다.
일반 상대성 이론은 실험적으로 성공적이나, 이를 주로 양자장론과 관련하여 여러 가지로 확장할 수 있다.
일반상대론에 비틀림을 더한 이론은 아인슈타인-카르탕 이론이고, 중력상수를 스칼라장으로 승진시키면 브랜스-딕 이론을 얻는다.
일반 상대성 이론에 추가 차원을 도입하여 다른 상호작용을 포함시키는 이론은 칼루차-클라인 이론이며, 초대칭을 도입하면 초중력 이론을 얻는다.
또한 초끈이론에서는 아인슈타인-힐베르트 작용을 자연스럽게 얻을 수 있으며, 고리 양자 중력에서는 아인슈타인-힐베르트 작용을 가지고 이를 양자화 한다는 것에서 시작한다.
○ 특수 상대성이론 (特殊相對性理論, theory of special relativity)
특수 상대성이론 (特殊相對性理論, theory of special relativity) 또는 특수상대론 (特殊相對論, special relativity)은 빛의 속도에 견줄 만한 속도로 움직이는 물체들을 다루는 역학 이론이다.
특수 상대성 이론은 고속의 물체에 대하여 기존의 뉴턴 역학의 갈릴레이 변환을 대체하고, 갈릴레이 변환과 달리 고전전자기학의 맥스웰 방정식과 일관적이다.
특수 상대성 이론은 갈릴레이 변환 대신 로런츠 변환을 채용한다. 이 이론에서는, 갈릴레오가 주장한 것처럼 모든 관성계가 동등하지만, 전자기학의 맥스웰 방정식과 일관하게 광속이 모든 관성계에서 동등하다. 즉, 빛 (혹은 다른 질량이 없는 입자)의 속도는 이를 방출하는 물체와 관찰자 사이의 상대운동에 무관하다.
특수 상대성 이론은 여러 가지 놀라운 예측을 하는데, 이 예측들은 전부 실험에 의해 검증되었다. 로런츠 변환을 도입함에 따라, 시간과 공간을 운동학적으로 더 이상 구별하여 생각할 수 없다.
헤르만 민코프스키는 이 둘을 더하여 시공간이라는 하나의 개체로 생각하고 기하학적으로 다루는 민코프스키 공간을 도입하였다. 이에 따라, 시간과 공간 중 하나에만 의존하는 측정량 (예를 들어 길이, 시간 간격 등)은 서로 다른 관성계에서 서로 다른 값을 가진다. 따라서, 시간과 공간에 해당하는 값들을 합쳐서 4차원 벡터로 나타내면 다루기 쉽다.
특수 상대성 이론에서는 어떤 일반적 속도 상수(광속)가 존재하므로, 이를 이용하여 질량과 에너지를 관계지을 수 있다. 이론에 따르면, 어떤 계의 질량은 그 계의 운동량 중심의 (순간적인) 관성계에서의 에너지와 같다 (E = mc2). 이를 질량-에너지 등가성이라 한다.

특수 상대성 이론은 (뉴턴 역학과 같이) 상대성 원리를 오로지 관성계에 대해서만 적용한다. 즉, 가속계는 관성계와 실험적으로 구별할 수 있다는 것이다. 후에 발견된 일반 상대성 이론은 중력을 고려하면 가속계가 관성계와 동등하다고 주장한다 (정확히 말하면, 가속계와 관성계를 구별할 수 없다).
그러나 강한 중력장이 없는 경우, 특수 상대성 이론은 물리적 현상을 정확히 기술한다. 다루어지는 속도가 빛의 속도에 비해 훨씬 작은 일상적인 영역에 대해서는 특수 상대성 이론의 예측은 뉴턴 역학의 예측과 일치한다고 한다.
특수 상대성 이론의 결론은 다음과 같이 요약할 수 있다.
- 관측자에 대해 빠른 속도로 운동하는 물체는 시간이 느려진다(시간 지연).
- 관측자에 대해 빠른 속도로 운동하는 물체는 고전적 운동량보다 더 큰 값을 가진다.
- 관측자에 대해 빠른 속도로 운동하는 물체는 길이가 짧아진다.
- 질량이 에너지로, 혹은 에너지가 질량으로 바뀔 수 있다.(E=mc2)

참고 = 위키백과
크리스천라이프 편집부

