세차 운동 (歲差運動, precession), 옆돌기 운동

세차 운동 (歲差運動, precession), 옆돌기 운동

세차운동 (歲差運動) 또는 ‘옆돌기운동’은 회전하는 천체나 물체의 회전축이 도는 형태의 운동이나 그 현상을 말한다.

○ 물리학

물리학에서 세차운동 (precession)은 회전하고 있는 강체에 돌림힘이 작용할 때, 회전하는 물체가 이리저리 흔들리는 현상을 말한다. 세차운동을 관찰할 수 있는 가장 일반적인 예는 팽이를 돌릴 때, 회전 속도가 줄면서 팽이의 축을 중심으로 한 팽이의 회전이 아닌 축 자체가 팽그르르 도는 것이다.

팽이뿐만 아니라 특정 축을 중심으로 자전하는 물체는 중력이 작용하는 지구상에서 모두 세차운동을 할 수 있다. 회전하는 팽이가 세차운동을 할 때에, 팽이의 회전축은 물체의 회전 방향과 반대방향으로 돌게 된다. 세차운동 동안 회전속도와 작용하는 돌림힘이 일정하다면, 축이 이동하는 속도는 돌림힘과 각속도 (회전축의 방향)와 계속 직각이 되어 회전하는 축이 그리는 자취는 원뿔이 된다.

팽이의 축이 완벽히 중력 방향이 아니고 약간 기울어져 있다면, 중력은 팽이를 넘어뜨리려고 잡아끈다. 이 힘은 팽이의 아랫쪽 끝을 축으로 무게중심을 아랫쪽으로 돌리려는 토크로 작용한다. 그러나 팽이는 기울어진 방향으로 그대로 넘어지지 않고, 기울어진 태우만 회전하게 된다.

○ 지구의 세차 운동

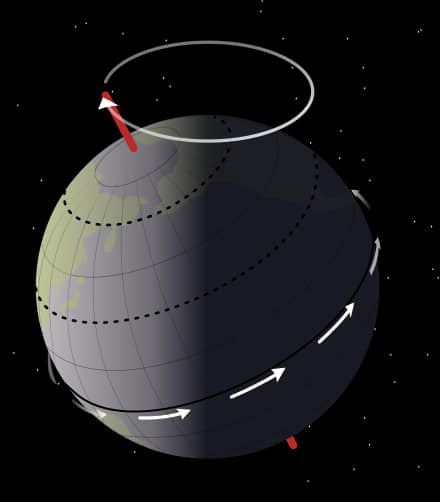
지구도 회전하는 강체로 볼 수 있기 때문에 세차 운동이 생긴다. 지구는 극반지름에 비해 적도반지름이 조금 더 큰 회전타원체 모양을 하고 있다. 부풀어 오른 부분을 벌지 (bulge)라고 한다. 거리가 멀어질수록 작아지는 중력의 특성 때문에 태양의 중력은 태양을 향한 쪽 벌지에서 더 크게 작용하게 된다. 지구의 자전축이 지구의 공전궤도면에서 기울어져 있기 때문에 하지나 동지 무렵에는 벌지에 작용하는 태양의 중력 차이가 지구를 공전궤도면에 수직으로 세우려는 힘 (돌림힘)으로 작용하게 된다. 회전하는 계에 돌림힘이 작용하면 돌림힘 방향의 각운동량을 더하게 된다. 지구의 경우에는 태양과 지구의 벌지때문에 생기는 돌림힘은 춘분점 방향과 평행하므로 지구의 회전축은 춘분점 방향으로 기울게 된다. 그만큼 춘분점은 다시 이동하게 되어 같은 작용이 반복되므로 지구 자전축은 회전하게 되는 것이다. 한 세기 동안의 관찰 결과에 의하며 춘분점은 일년에 50.3초만큼 이동하며 360도를 이 값으로 나누면 주기는 약 25,765년4개월27일 정도가 된다. [일반세차의 영향으로 지구의 자전축이 천구를 한바퀴도는 데 걸리는 시간이 대략 25,800년이라고 서술된 책이 많은 데, 이는 2000.0년기준의 세차상수 (5028.796195″ /36525일당)를 기준으로 역산한 값으로 근사치일 뿐이며, 실제로 더 정확한 값을 , J.Laskar, F.Joutel, F.Boudin (1993)의 “Orbital, precessional and insolation quantities for the Earth from -20Myr to +10Myr”의 데이터를 기준으로 구해보면, 2000.0년기준으로 25,436년 224일 16시간(25436.61511년)이 된다.]

19세기 전반기에 행성들도 지구의 세차에 영향을 미친다고 결론내려졌다. 19세기 후반에 태양과 달의 중력에 의한 세차를 일월세차라 명명했고, 행성의 중력에 의한 세차를 행성 세차라 명명했다. 그리고, 그 두 요소의 합을 일반세차라고 불렀다. 현재 일월세차는 행성세차보다 약 500배 더 큰 것으로 알려져 있다.

지금의 지구 자전축은 작은곰자리의 알파별을 향하고 있지만 기원전 15세기의 이집트 사람들이 관찰할 당시에는 용자리의 알파별이었다. 그리스의 히파르코스는 기원전 120년에 이전 천문학자들의 관측과 자신의 관측을 종합하여 세차운동을 발견하였다.

○ 자전축의 세차운동

자전축의 세차운동 (自轉軸之 歲差運動, axial precession)은 천문학에서 천체의 자전축의 방향에서 일어나는 중력으로 인한 느리고 연속적인 변화이다. 그것은 거의 대칭적으로 꼭짓점이 연결된 한 쌍의 원뿔의 모서리를 따라서 흔들리는 대각선 끝을 연상케 하는데, 특히, (점성술에서 대년 또는 플라톤 년이라고 불리는) 거의 26,000년의 주기 동안에 지구의 자전축의 방향에서 일어나는 점진적인 이동을 일컫는다. “세차”의 용어는 일반적으로 이러한 큰 영년변화를 일컫는데만 사용된다. 참고로, 지구 자전축의 정렬에서 일어나는 보다 작은 규모의 다른 변화로는 장동과 극운동이 있다

역사적으로 지구의 세차운동은 분점의 세차운동 (分點之 歲差運動, precession of the equinoxes) 이라고 불렸다. 왜냐하면, 분점이 황도를 따라 항성에 비해서 서쪽으로 즉, 황도를 지나는 태양의 이동 방향과 반대로 움직였기 때문이다. 이 용어는 상세한 수학적 계산이 결여된 비전문적 논고에서 여전히 사용된다. 히파르코스는 세차운동에 대해서 기록했는데, 쐐기 문자 평판에서 비롯된 증거가 그의 서술과 수학적 계산이 여러 세기 이전부터 존재해 왔던 바빌로니아의 천문수학에 몹시 의존했음을 시사하는데도 불구하고, 역사적으로, 그것을 그가 발견한 것으로 인정되고 있다. 그의 생애의 정확한 기간은 알려지지 않았지만, 프톨레마이오스에 의한 천문학 관측은 그가 기원전 147년부터 기원전 127년에 활동했다고 본다.

19세기의 전반기 동안에 행성과 그것들 사이의 중력을 계산하는 능력이 향상됨에 따라, 그 힘도 황도를 조금씩 움직이게 한다고 인정되었고, 1863년에 그것은 행성 세차 (行星 歲差, planetary precession)라는 명칭이 붙었는데, 반면에 우세한 요소는 일월세차 (日月歲差, lunisolar precession)라는 명칭이 붙었다. 그것들의 결합에는 분점의 세차 대신에 일반 세차 (一般 歲差, general precession)라는 명칭이 붙여졌다.

일월세차는 지구의 적도융기에 미치는 달과 태양의 중력에 의해 발생하며, 관성 공간에 대한 지구의 자전축의 이동을 야기한다. 행성 세차 (전진)는 지구에 미치는 다른 행성의 중력과 그 궤도면 (황도) 사이의 작은 각도로 인한 것으로, 관성 공간에 대한 황도면의 다소의 이동을 야기한다. 일월세차는 행성 세차보다 약 500배 더 크다. 태양과 달에 부가적으로, 행성이 지구 자전축의 관성공간에 대한 근소한 이동을 야기한다는 사실에 비해, 오인의 소지가 있을만큼 일월세차 대 행성 세차로 용어가 서로 대조되었는데, 따라서, 2006년에 국제천문연맹은 우세한 요소가 재명명되기를 권고했고, 주요소를 적도의 세차운동 (赤道之 歲差運動, precession of the equator)이라고 명명하고, 부요소를 황도의 세차운동 (黃道之 歲差運動, precession of the ecliptic)으로 명명했다. 그러나, 그것들의 결합은 여전히 일반 세차로 명명되어 있다. 그 정정이 있기 전에 출판된 서적들에는 옛 용어를 사용한 많은 언급이 있다.

– 세차의 명명법

세차운동의 영문 용어는 프리세션 (precession) 인데, 직역하면 선행 (先行)이다. 어원학적으로 선행 (precession)과 행진 (procession)은 (라틴어로 앞으로 행진하는 전진 [前進]을 뜻하는 단어 processio에서 파생되었고) 운동과 관계된 용어이다. 일반적으로 용어 행진은 객체의 한 무리가 앞으로 움직이는 것을 묘사할 때 사용되며, 반면에, 용어 선행은 객체의 무리가 뒤로 움직이는 것을 묘사할 때 사용되는 용어이다. 지구의 일주 운동으로 인하여 날마다 그리고 태양에 대한 지구의 공전으로 인하여 매년마다 지구로부터 관찰되는 항성은 동쪽에서 서쪽으로 전진되는 것으로 보인다. 같은 시간에서 보면, 항성은 매년마다 거의 50 각초의 비율로 약간씩 역행하는데, 그 현상은 “분점의 세차운동”으로 알려져 있다.

그러한 운동을 설명하는데 있어서, 천문학자들은 일반적으로 그 용어를 “precession (선행)”으로 축약한다. 그리고, 그 운동의 원인을 설명하는데 있어서, 물리학자들 또한 같은 용어를 사용하는데, 천문학에서는 어느 종류의 선행은 실제적인 것이며 다른 것은 외견적인 것이라는 점에서, 관측되는 현상과 그것의 원인 사이에 다소 혼동이 유발된다. 그러한 문제는 대부분의 천문학자들이 물리학자나 천체 물리학자라는 사실에 의해 더욱더 애매해진다.

천문학에서 사용되는 “선행”이라는 용어는 일반적으로 관측되는 (하늘에서 항성이 역행하는) 분점의 선행을 설명하며, 반면에, 물리학에서 사용되는 “선행”이라는 용어는 일반적으로 역학적 과정을 설명한다는데 유념할 필요가 있다.

한자어인 세차 (歲差)는 지구에서 볼 때, 항성에 관한 하늘과 절기를 만드는 태양에 대한 하늘 사이에 차이가 나게됨을 일컫는다. 황도 좌표계에서 그 차이는 항성 황도대와 회귀 황도대 사이의 차이이다. 세차운동은 자전축이나 춘분점이 이동하는 현상을 일컫는 천문학 용어이다.

– 역사

*헬레니즘 세계

.히파르코스

기원전 280년 경에 이미 사모스의 아리스타르코스가 항성년과 회귀년의 다른 값을 갖고 있었다는 여전히 논쟁의 여지가 있는 증거에도 불구하고, 세차운동의 발견은 일반적으로 로도스의 또는 니케아의 그리스 천문학자 히파르코스 (기원전 190~120년)에 의한 것으로 인정된다. 클라우디오스 프톨레마이오스의 알마게스트에 따르면, 히파르코스가 스피카와 그 외의 밝은 항성들의 경도를 측정했다고 한다. 그는 그의 전임자 티모카리스 (기원전 320~260년)와 아리스틸루스 (기원전 ~280년)의 자료를 그의 측정치와 비교했는데, 스피카가 추분점에 대하여 2° 움직여 왔다는 결론을 얻었다. 그는 (태양이 춘분점으로 복귀하는데 걸리는 시간인) 회귀년과 (태양이 한 개의 항성으로 복귀하는데 걸리는 시간인) 항성년을 비교하기도 했는데, 근소한 차이를 발견했다. 히파르코스는 춘분점이 황도대를 통해 이동 (“세차운동”)되었으며, 세차의 비율은 한 세기에 1° 보다 작지 않다는, 다른 말로 하면, 36000년 보다 더 길지 않은 시간 동안 한 번의 완전한 주기를 완주한다는 결론을 내렸다.

사실상 히파르코스의 기록은 세차운동에 대한 그의 업적을 포함해서 모두 소실되었다. 그것들은 정지한 지구를 중심으로 하는 천구의 공전으로 세차운동을 설명한 프톨레마이오스에 의해서 언급되었다. 히파르코스는 프톨레마이오스와 마찬가지로 지구보다 하늘이 움직이는 지구중심설에 한해서 세차운동에 대해 생각했다고 추정함이 타당하다.

.프톨레마이오스

히파르코스의 세차운동에 관한 연구를 계속 이어나간 것으로 알려진 최초의 천문학자는 2세기의 프톨레마이오스이다. 프톨레마이오스는 월식을 요하지 히파르코스의 달을 사용한 방식의 변형으로 레굴루스와 스피카 등의 밝은 항성들의 경도를 측정했다. 일몰 전에, 그는 태양으로부터 멀어지는 달의 경도를 측정했다. 그 다음, 일몰 후에, 그는 달부터 항성까지의 경도를 측정했다. 그는 태양의 경도를 계산하는 히파르코스의 방식을 사용했고 달의 이동과 그것의 시차를 정정했다. 프톨레마이오스는 그의 관찰 결과와 히파르코스와 메넬라우스, 티모카리스 그리고 아그리파의 값들과 비교했다. 그는히파르코스와 그의 시간의 차이 (약 265년)와 항성이 2°40′ 또는 100년에 1°씩 (1년에 36″씩: 오늘날 이 비율은 1년에 약 50″ 또는 72년에 1° 씩이다.) 이동해왔음을 발견했다. 그는 세차운동이 모든 항성에게 적용되지만, 황도에 인접한 천체에게는 그렇지 않음을 확증했는데, 그의 주기는 히파르코스가 계산한 값과 같은 36000년의 기간이었다.

.다른 저자들

대부분의 고대 작가는 세차운동을 언급하지 않았는데, 아마도 그것에 대해 모르고 있었던 듯싶다. 그러한 작가들로는 프톨레마이오스 외에 세차운동을 부정한 프로클루스와 프톨레마이오스의 설명을 수용한 4세기의 프톨레마이오스의 주석자 알렉산드리아의 테온을 들을 수 있다. 테온은 대안적 이론을 공표하기도 했다.

어떤 견해에 따르면, 고대의 점성가들은 특정 시대로부터 지일의 별자리가 그 별자리의 위치에서 8° 움직였다고 믿었다. 그후에 그것들은 같은 곳으로 복귀하고 … “진동하는” 분점은 황도대의 전체 경로를 통해서 진행하는 대신에, 8°의 호 만큼을 전후로 움직인다는 진동의 이론이 테온에 의해 세차운동의 대안으로써 제안되었다.

*대안적 이론

.바빌로니아

히파르코스와 관계없이 세차운동을 발견해온 다른 문화권들에서의 각개의 주장이 있다. 알바타니에 따르면, 칼데아의 천문학자들은 회귀년과 항성년을 구별해왔었는데, 부정확하더라도, 거의 기원전 330년에,그것들은 세차운동이 설명되는 위치에 있게 될 것이라고 했지만, 그와 같은 주장이 일반적으로 옹호되지는 않았던 것으로 여겨진다.

.고대 이집트

히파르코스의 시대 이전에 고대 이집트에서 알려진 세차운동에 대한 유사한 주장들이 있었지만, 그러한 주장들은 논쟁의 여지가 있는 채로 남아 있었다. 예를 들어, 주장된 바에 의하면, 카르나크 신전 단지에 있는 몇몇 건물이 한 해의 중요한 때에 특정 항성들이 떠오르거나 저무는 지평선의 한 점을 향하여 건축 되었다고 한다. 몇 세기 이후에, 세차운동이 방향성을 구식으로 만들면, 그 신전은 재건축되었다. 그러나, 항성의 정렬이 오차가 생겼다는 관찰은 이집트인들이 항성이 황도에서 하늘을 가로지르며 72년에 약 1도씩의 일정한 비율로 이동함을 이해했다는 의미가 아니다. 그렇지만, 그들은 정확한 달력을 보유하고 있었고, 만일 그들이 신전의 재건축 기간을 기록했었다면, 대략적인 세차운동의 비율을 계산하는 것은 간단한 문제였을 것이다. 후기 (프톨레마이오스) 시대부터 덴데라에 있는 하토르 신전의 항성 지도인 덴데라 황도대는 분점의 세차가 기록된 것으로 추정된다. 아무튼, 고대 이집트인들이 세차운동에 대해서 알고 있었다고 하더라도, 그들의 지식은 현재까지 잔존하는 천문학 문헌에는 기록되어 있지는 않다.

마이클 라이스는 그의 저서 ‘이집트의 유산’ (Egypt’s Legacy)에서 “비티니아인 히파르코스에 의한 새차운동의 정의 이전에 고대인들이 그것의 역학을 알았었는지의 여부는 불분명하지만, 밤하늘에 대한 헌신적인 관찰자들로서 그들은 그것의 효과를 간과할 수 없었다.”(128쪽)고 한다. 라이스는 “세차운동이 이집트의 발전을 촉진한 것을 이해하는데 기초가 된다”(10쪽)고 인정하며, “어떤 의미에서는, 국민국가로써의 이집트와 살아있는 신으로서의 이집트 왕은 이집트인들이 세차운동이 수반하는 천체의 막대한 외견상 이동에 의해 야기되는 천문적 변화를 깨달은 결과이다.”(56쪽)라는 범위로 확대해서 생각한다. 카를 구스타프 융에 따르면, 라이스는 “기자에 있는 피라미드가 주요 위치를 향해 정렬된 정확도와 항성에 맞춰 그것들의 정렬을 이루어 건축될 수 있었던 정확성으로 인하여, 기원전 제3천년기에 (그리고 어쩌면 그 이전에도) 이집트에서 매우 정밀한 천문적 관찰이 실시되었다는 증거가 명확해진다고 한다. 그러한 사실만으로도 이집트인들의 세차운동의 지식에 대한 융의 믿음을 이전에 그럴 듯하게 여겨졌던 것보다 훨씬 덜 추측적이게 만든다.”(31쪽)고 한다. 라이스는 “이집트인들은 세차운동의 결과로 인하여, 본래에 있었던 신전에 대한 항성의 위치가 이동되었을 때, 신전의 방향을 개조하기도 했는데, 새로운 왕조의 치세기 동안에 그러한 일들이 여러 차례 일어난 듯하다.”(170쪽)고 한다.

수 천년 이상 고대 이집트의 사제적 엘리트가 세차적 주기를 추적했다는 개념은 로버트 보벌과 그레이엄 핸콕에 의해 그들의 1995년 저서 ‘창세의 수호신’ (Keeper of Genesis)에서 상술된 이론들의 중심적 역할을 한다. 그 저자들은 고대 이집트의 기념적 건축물들이 하늘의 지도로써 기능했으며, 연관된 제식은 천체의 사건에서 우러난 현세의 정묘한 활동이었다고 주장한다. 특히, 그 의식은 제프 테피 (“최초의 시간”)으로 알려진 먼 조상의 시대로 세차적 주기가 “되돌아 옴”을 상징했는데, 저자들은 그 때를 기원전 10,500년경으로 계산했다. 그 추정값은 저자들이 이집트인들의 기록이 시작 되었다고 인정하는 연도이다. 선사 시대의 이집트에 대한 연구로부터 비롯된 증거는 수렵채집으로부터 중앙집권화된 사회의 질서로 농경에 기반한 정착을 이끈 이집트 지역 거주자들의 문화에서 발생한 주요 변화를 입증한다. 그 변화는 기후변화와 과방목으로 인해 유발되어왔었던 듯하다.

.마야

메소아메리카의 장주기력이 어떻게든 세차운동에 대하여 조정되었다는 추측이 있지만, 그 견해는 전문적인 마야 문명을 연구하는 학자들에게는 수용되지 않는다. 그러나, 밀브레이스는 “플레이아데스를 포함하는 30,000년의 장주기년은 … 춘분점의 세차운동을 계산하려는 노력이 되어왔을 수도 있다.”고 전했다.

.인도

12세기 바스카라 2세의 문헌은 이렇게 전한다. ‘수리야싯단타’에 따르면, 43억2천년의 1칼파 동안에 삼파트는 30,000번을 음회전하고, 반면에, 문잘라 등은 1칼파 동안에 아야나가 199,669회 전진하며, 하나는 상승과 하강의 차이 등을 규명하기 전에 두 가지의 조합이 있어야 한다.” 랜슬럿 윌킨슨은 완전한 의미를 전달하는 너무도 간단한 어문으로 된 그 세개의 절의 마지막을 번역했는데, 현대 힌디어 주석서에서 표면화해온 두 가지의 조합 부분을 생략했다. 힌디어 주석서에 의하면, 세차 주기의 마지막 값은 야야의 +199,669번의 회전과 삼파트의 −30 000번의 회전을 더함으로 한 칼파당 +169,669이 산출되도록 구해져야 한다.

게다가, 문잘라의 값은 아야나의 이동에 21,636년의 한 주기를 부여하는데, 그 값은 근일점 세차운동도 계산에 포함될 때의 현대적 세차 값이다. 후자는 현재 136,000년의 주기를 지니지만, 바스카라 2세는 그 값을 144,000년 (1칼파에 30,000번)으로 보았고 그것을 삼파트라 칭했다. 바스카라 2세는 음의 삼파트에 양의 아야나를 조합한 후의 마지막 용어의 이름을 정하지 않았다. 그러나, 그가 부여한 값은 그가 아야나에 의해 궤도상 근일점 세차가 조합된 효과를 고려한 세차운동을 계산했으며, 삼파트에 의해 근일점 주기를 계산했지만, 그것을 그것을 분점으로 한정하지는 않았음을 나타낸다. 그는 그의 업적인 싯단타 쉬로마니를 명확화한 바사나바쉬아 주석서에서 수리야싯단타는 가용될 수 없으며 그가 전문에 근거해서 기술 한다고 밝힌 점에서, 그의 문체는 다소 혼동이 야기된다. 바스카라 2세는 그 자신의 견해를 기술하지 않았으며, 단지 수리야싯단타와 문잘라 그리고 이름 없는 “다른 것들”을 인용했을 뿐이다.

전통적 주석자들에 따르면, 현존하는 수리야싯단타는 ±27°의 범위 안에서 1년에 54″씩의 비율로 진동하는 개념을 옹호한다. 하지만, 버제스는 그가 바사카르 2세에 의해 언급된 수리야싯단타를 인용한 데서 본래의 의미는 순환적 운동에 대한 것이 틀림없다는 의견을 더했다.

.중국의 우희

우희 (虞喜, 281~356)는 세차운동을 언급한 최초의 중국 천문학자이다. 그는 50년에 1°씩의 비율로 세차의 비율을 추산했다.

*중세와 르네상스

중세 이슬람의 천문학에서, 마라게 천문대에서 편찬된 ‘지즈이 일카니’는 분점의 세차를 세 년당 51각초로 정했는데, 그 값은 현대의 값인 50.2각초와 매우 근접한다.

중세에, 이슬람과 라틴의 기독교 천문학자들은 그러한 “진동”을 세차가 더해지는 항성의 이동으로 간주했다. 그러한 이론은 일반적으로 아랍의 천문학자 타비트 이븐 쿠라에 의한 업적으로 간주되지만, 그러한 간주는 현대에 논쟁되어오고 있다. 니콜라우스 코페르니쿠스는 ‘천구의 회전에 관하여’ (De revolutionibus orbium coelestium, 1543년)에서 진동의 다른 계산법을 내놓았다. 그 저서는 세차를 지구 자전축의 이동의 결과로 확신한 최초의 문헌이다.

*현대

한 세기가 지나고 세차운동은 아이작 뉴턴의 ‘자연철학의 수학적 원리’ (Philosophiae Naturalis Principia Mathematica, 1687년)에서 중력의 결과라고 설명되었다. 뉴턴의 세차에 관한 최초의 균차가 사용되지는 않았지만, 장 르 롱 달랑베르와 그 이후의 과학자들에 의해서 적지않게 교정되었다.

– 히파르코스의 발견

히파르코스는 ‘지점과 분점의 이동에서’ (On the Displacement of the Solsticial and Equinoctial Points, 알마게스트 3권 1장과 7권 2장에서 묘사됨)에서 그의 발견을 설명했다. 그는 월식 동안의 항성 스피카의 황도상 경도를 측정했고 그것이 추분점에서 서쪽으로 6° 쯤에 있음을 알았다. 그는 (기원전 3세기에 아리스틸루스와 함께 작업했던 에우클레이데스와 동시대의) 알렉산드리아의 티모카리스의 측정값과 자신의 것을 비교하여, 스피카의 경도가 약 150년 동안에 2° 가량 감소했음을 알았다. 그는 다른 항성의 이동에도 주목했다. 그는 황도와 인접한 항성만이 시간이 흐르면서 이동한다고 추측했다. 프톨레마이오스는 그것을 “첫 번째 가설” (알마게스트 제7권 1장)이라 칭했지만, 히파르코스가 고안한 것으로 알려진 어떤 가설도 공표하지는 않았다. 히파르코스는 매우 신뢰되지는 않는 근과거의 관측값만을 가지고 있었기 때문에, 그의 가설에 분명히 제한을 두었다.

왜 히파르코스는 항성의 위치를 측정하는데 월식을 필요로 했는가? 주야 평분점은 하늘에 표시되지 않았으므로, 그는 달을 참조점으로 사용했다. 히파르코스는 이미 어떤 순간의 태양의 경도를 계산할 수 있는 방법을 개발했었다. 달이 충에 있을 때, 보름달 동안에 월식이 일어난다. 식의 중간점 때에, 달은 태양으로부터 정확히 180°에 위치한다. 히파르코스는 그 때의 달로부터 스피타의 경도 차이를 측정했던 것이다. 그는 그 값에 달과의 경도 차인 180°를 더해서 계산된 태양의 경도값을 더했다. 그는 티모카리스의 자료와 같은 절차로 작업하지 않았다. 덧붙여 말하면, 히파르코스에 대한 전기적 정보는 드물기 때문에, 월식을 사용한 그러한 관측은 그의 작업이 언제 이루어졌는지에 대한 주요한 근거 자료가 된다. 예를 들어, 그가 관측한 월식은 기원전 146년 4월 21일과 기원전 135년 3월 21일에 일어났다.

히파르코스는 ‘한 해의 길이’ (On the Length of the Year)에서 세차운동을 연구하기도 했다. 두 가지의 년이 그의 업적을 이해하는 것과 관련된다. 회귀년은 지구로부터 보는 관점에서, 태양이 황도 (천구의 항성들 사이에 있는 경로)를 따라 같은 위치로 복귀하는데 걸리는 시간의 길이이다. 항성년은 천구의 항성을 기준으로 태양이 같은 위치로 복귀 하는데 걸리는 시간의 길이이다. 세차운동은 매년마다 항성의 경로를 약간씩 변하게 하므로, 항성년이 회귀년보다 길다. 분점과 지점의 관측을 활용한 히파르코스는 회귀년의 길이를 365+1/4−1/300일 또는 365.24667일로 계산했다. 그는 그 값을 항성년의 길이와 비교해서 세차의 비율을 1°보다 적지 않은 값으로 산정했다. 그 정보로부터 항성년의 값을 계산하면, 365+1/4+1/144일 또는 365.25694일 나온다. 현대의 것과 비교하면, 그의 측정 값은 약간의 오차가 있다.

그는 ‘윤달과 윤일에 대하여’ (On Intercalary Months and Days, 현재 소실)에 있는 메톤과 칼리포스의 달력을 수정하여 그의 회귀년과 근접한 태음태양력을 만들었는데, 그것은 프톨레마이오스에 의해 알마게스트 제3권 제1장에서 소개 되었다. 바빌로니아 달력은 기원전 499년 부터의 235년의 (기원전 380년전에 단 세 번의 예외가 있는) 19년에 235개의 태음월 주기를 사용하지만, 구체적인 날 수가 규정되지 않았다. 메톤 주기 (기원전 432년)은 19년에 6.940일을 할당하여 연평균 365+1/4+1/76일 또는 365.26316일씩을 산출한다. 칼리푸스 주기 (기원전 330년)는 연평균 약 365+1/4일 또는 365.25일이 되도록 4 메톤 주기 (76년)에서 하루를 생략한다. 히파르코스는 4 칼리푸스 주기 (304일)에서 하루를 더 감해서 연평균 일수를 365+1/4−1/304일 또는 365.24671로 하는 히파르코스 주기를 만들었는데, 그 일수는 365+1/4−1/300 또는 365.24667일인 그의 항성년에 근접했다. 그리스의 이 세 가지 주기는 어떤 상용력에서도 사용된 적이 없었고, 오직 ‘알마게스트’와 같은 천문학 문헌에서만 등장할 뿐이다.

우리는 기원전 2세기의 고대 천문학 컴퓨터인 안티키테라 메커니즘에서 히파르코스의 수리적 특징을 알 수 있다. 그 메커니즘은 하늘에서 (거의 19년만에 같은 위치에 나타나는 보름달로써) 달이 같은 위상으로 같은 항성에 재등장하는 주기인 메톤 주기와 (4 메톤 주기이며 더 정확한) 칼리푸스 주기, 사로스 주기 그리고 (식의 정확한 예측을 위해서 사용되는 3 사로스 주기의) 엑셀리그모스 주기의 태양년을 기초로 한다. 안티키테라 메커니즘에 대한 연구는 고대인들이 하늘에서의 태양과 달의 이동에 관한 모든 위상에 기반하는 매우 정확한 달력을 사용하고 있었음을 증명한다. 사실, 안티키테라 메커니즘의 일부인 달의 메커니즘은 케플러의 제2법칙과 매우 근접한 달의 변화하는 속도가 적용된, 예를 들어, 그것은 근일점에 있는 달의 가장 빠른 이동과 원일점에 있는 가장 느린 이동을 계산에 넣은, 핀과 슬롯 장치가 있는 일련의 네 개의 기어를 사용하여 주어진 시간의 달의 이동과 위상의 변화를 표현한다. 그것의 발견은 히파르코스가 케플러의 제2법칙과 거의 유사한 것을 고안했다는 증거로써, 그의 수학적 계산들이 프톨레마이오스가 그의 저서에서 설명한 것보다 더 진보되었음을 입증한다.

크리스천라이프 편집부